Chapter 9
Probability and Variability
By Boundless
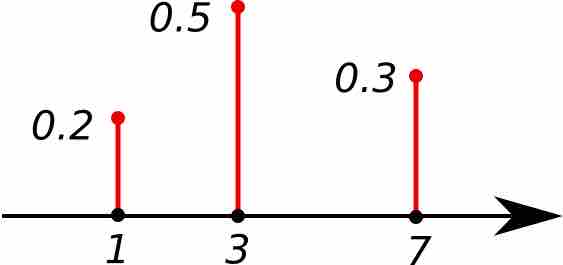
A random variable
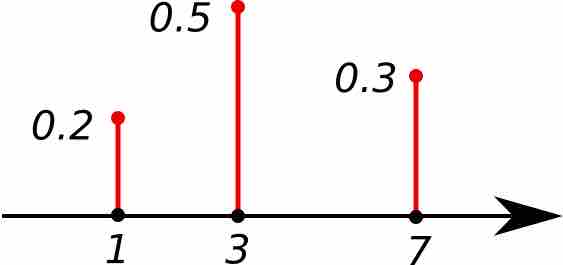
Probability distributions for discrete random variables can be displayed as a formula, in a table, or in a graph.
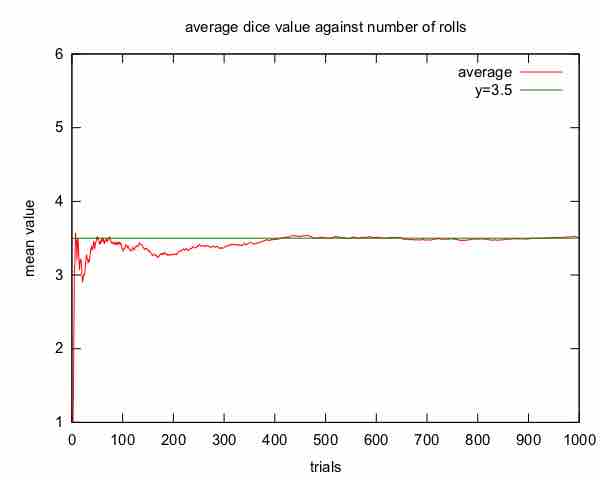
The expected value of a random variable is the weighted average of all possible values that this random variable can take on.
The binomial distribution is a discrete probability distribution of the successes in a sequence of
This chapter explores Bernoulli experiments and the probability distributions of binomial random variables.
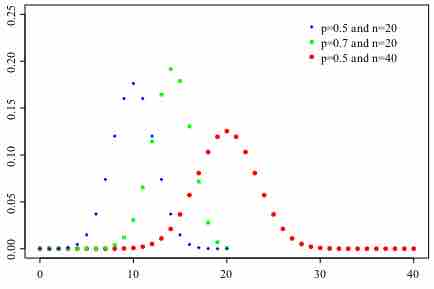
In this section, we'll examine the mean, variance, and standard deviation of the binomial distribution.
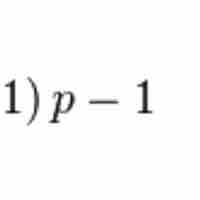
In this section, we'll look at the median, mode, and covariance of the binomial distribution.
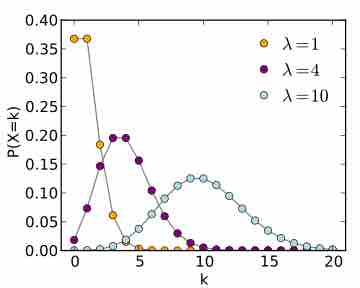
The Poisson random variable is a discrete random variable that counts the number of times a certain event will occur in a specific interval.
A hypergeometric random variable is a discrete random variable characterized by a fixed number of trials with differing probabilities of success.