Additional Properties of the Binomial Distribution

In general, there is no single formula for finding the median of a binomial distribution, and it may even be non-unique. However, several special results have been established:

If $np$ is an integer, then the mean, median, and mode coincide and equal $np$.

Any median $m$ must lie within the interval $\lfloor np\rfloor \leq m \leq \lceil np\rceil $.

A median $m$ cannot lie too far away from the mean: $|m np| \leq \min { \ln { 2 } } ,\max { (p,1 - p )}$.

The median is unique and equal to $m = round(np)$ in cases where either $p \leq 1 \ln 2$ or $p \geq \ln 2$ or $|m np| \leq \min{(p, 1 p)}$ (except for the case when $p = \frac{1}{2}$ and n is odd).

When$p = \frac{1}{2}$ and n is odd, any number m in the interval $\frac{1}{2} \cdot (n 1) \leq m \leq \frac{1}{2} \cdot (n + 1)$ is a median of the binomial distribution. If $p = \frac{1}{2}$ and n is even, then $m = \frac{n}{2}$ is the unique median.

There are also conditional binomials. If $X \sim B(n, p)$ and, conditional on $X, Y \sim B(X, q)$, then Y is a simple binomial variable with distribution.

The binomial distribution is a special case of the Poisson binomial distribution, which is a sum of n independent non-identical Bernoulli trials Bern(pi). If X has the Poisson binomial distribution with p1=…=pn=pp1=\ldots =pn=p then ∼B(n,p)\sim B(n, p).

Usually the mode of a binomial B(n, p) distribution is equal to where is the floor function. However, when $(n + 1)p$ is an integer and p is neither 0 nor 1, then the distribution has two modes: $(n + 1)p$ and $(n + 1)p 1$. When p is equal to 0 or 1, the mode will be 0 and n, respectively. These cases can be summarized as follows:

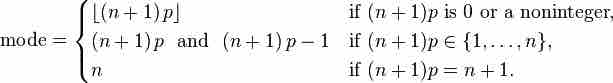
Summary of Modes

This summarizes how to find the mode of a binomial distribution.

Floor Function

Floor function is the lowest previous integer in a series.

Mode

This formula is for calculating the mode of a binomial distribution.

If two binomially distributed random variables X and Y are observed together, estimating their covariance can be useful. Using the definition of covariance, in the case n = 1 (thus being Bernoulli trials) we have .

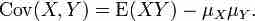
Covariance 1

The first part of finding covariance.

The first term is non-zero only when both X and Y are one, and μX and μY are equal to the two probabilities. Defining pB as the probability of both happening at the same time, this gives and for n independent pairwise trials .

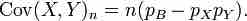
Covariance 3

The final formula for the covariance of a binomial distribution.

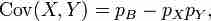
Covariance 2

The next step in determining covariance.

If X and Y are the same variable, this reduces to the variance formula given above.