Section 3
Limits
By Boundless
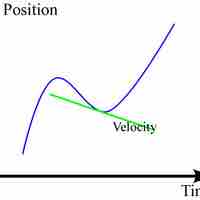
Iinstantaneous velocity can be obtained from a position-time curve of a moving object.
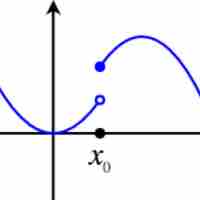
The limit of a function is a fundamental concept in calculus and analysis concerning the behavior of a function near a particular input.
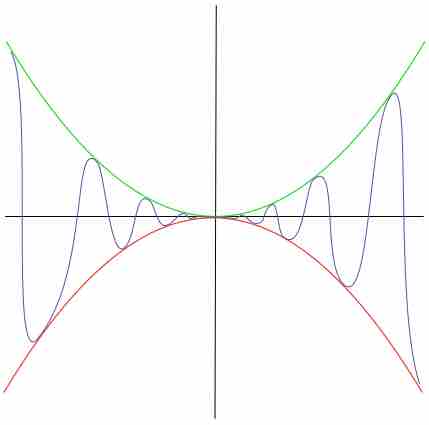
Limits of functions can often be determined using simple laws, such as L'Hôpital's rule and squeeze theorem.
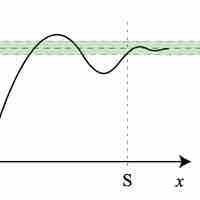
The
A continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output.
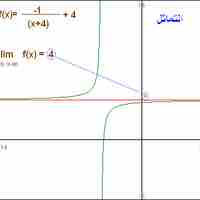
For a real-valued function expressed in terms of other functions, limit values may be computed via algebraic operations.
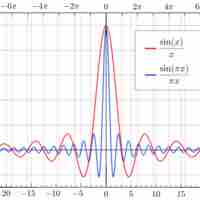
There are several limits of special interest involving trigonometric functions.
For a real-valued continuous function
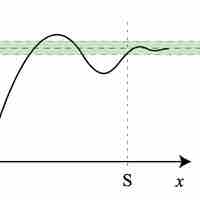
Limits involving infinity can be formally defined using a slight variation of the