Infinite Limits

Limits involving infinity can be formally defined using a slight variation of the $(\varepsilon, \delta)$-definition. For $f(x)$ a real function, the limit of $f$ as $x$ approaches infinity is $L$, denoted $\lim_{x \to \infty}f(x) = L$, means that for all $\varepsilon > 0$, there exists $c$ such that $\left | f(x) - L \right | < \varepsilon$ whenever $x>c$. Or, formally:

$\forall \varepsilon > 0 \; \exists c \; \forall x < c :\; \left | f(x) - L \right | < \varepsilon$

Infinite Limit

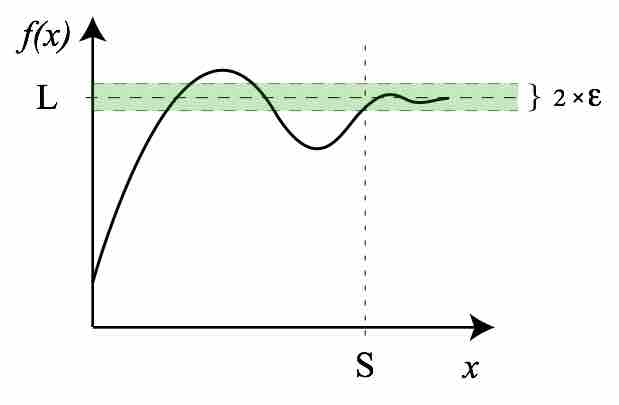
For any arbitrarily small $\varepsilon$, there exists a large enough $N$ such that when $x > N$, $\left | f(x)-2 \right | < \varepsilon$. Therefore, the limit of this function at infinity exists.

Similarly, the limit of $f$ as $x$ approaches negative infinity is $L$, denoted $\lim_{x \to -\infty}f(x) = L$, means that for all $\varepsilon > 0$ there exists $c$ such that $|f(x) - L| < \varepsilon$ whenever $x<c$.

For a rational function $f(x)$ of the form $\frac{p(x)}{q(x)}$, there are three basic rules for evaluating limits at infinity ($p(x)$ and $q(x)$ are polynomials):

1. If the degree of $p$ is greater than the degree of $q$, then the limit is positive or negative infinity depending on the signs of the leading coefficients;
2. If the degree of $p$ and $q$ are equal, the limit is the leading coefficient of $p$ divided by the leading coefficient of $q$;
3. If the degree of $p$ is less than the degree of $q$, the limit is $0$.

If the limit at infinity exists, it represents a horizontal asymptote at $y = L$. Polynomials do not have horizontal asymptotes; such asymptotes may however occur with rational functions.