The
The $(\varepsilon,\delta)$ -Definition
The
- For every real
$\varepsilon > 0$ , there exists a real$\delta > 0$ such that for all real$x$ ,$\varepsilon > 0$ $0 < \left | x-p \right | < \delta$ implies$\left | f(x) - L \right | < \varepsilon$ . Note that the value of the limit does not depend on the value of$f(p)$ , nor even that$p$ be in the domain of$f$ .
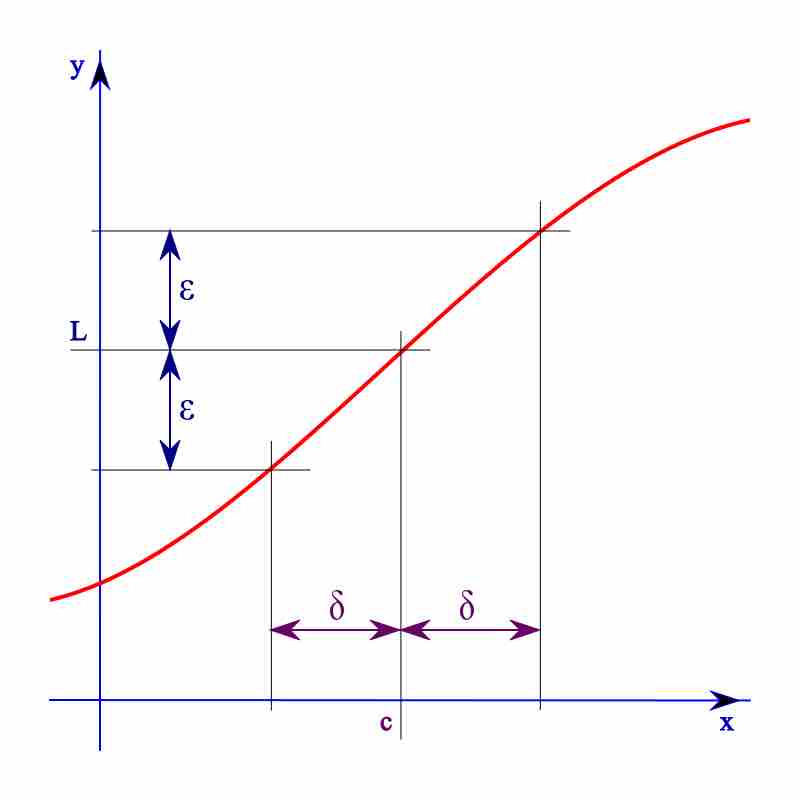
Definitely of a Limit
Whenever a point
Example
For an arbitrarily small
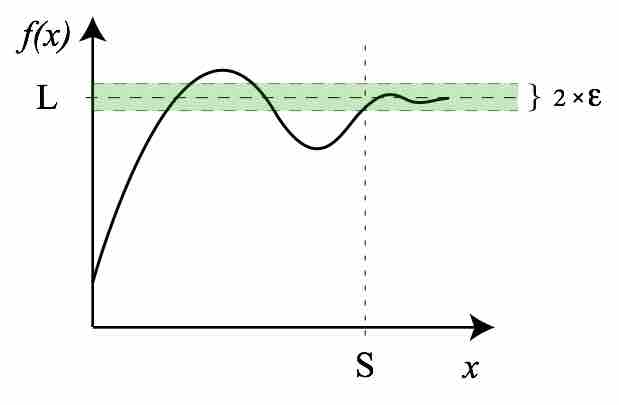
Limit of a Function at Infinity
For an arbitrarily small
The letters
This definition also works for functions with more than one input value. In those cases,