Linear Functions

Linear functions are algebraic equations whose graphs are straight lines with unique values for their slope and y-intercepts.

Slope describes the direction and steepness of a line, and can be calculated given two points on the line.

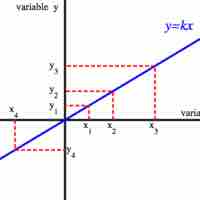
Two variables in direct variation have a linear relationship, while variables in inverse variation do not.

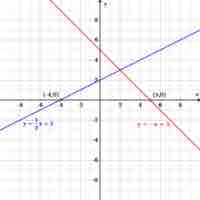
A zero, or $x$-intercept, is the point at which a linear function's value will equal zero.

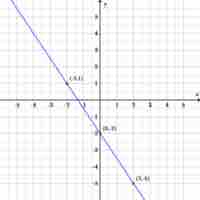
The slope-intercept form of a line summarizes the information necessary to quickly construct its graph.

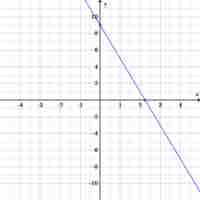
The point-slope equation is another way to represent a line; only the slope and a single point are needed.

Any linear equation can be written in standard form, which makes it easy to calculate the zero, or $x$-intercept, of the equation.

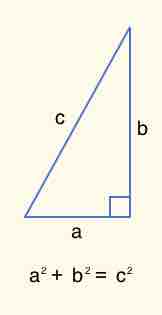
The distance and the midpoint formulas give us the tools to find important information about two points.

Parallel lines never intersect; perpendicular lines intersect at right angles.

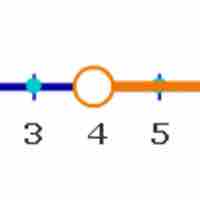
A linear inequality is an expression that is designated as less than, greater than, less than or equal to, or greater than or equal to.

Linear functions apply to real world problems that involve a constant rate.

Linear mathematical models describe real world applications with lines.

Curve fitting with a line attempts to draw a line so that it "best fits" all of the data.