File:Pythagoras by similar triangles.PNG

This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.

Summary

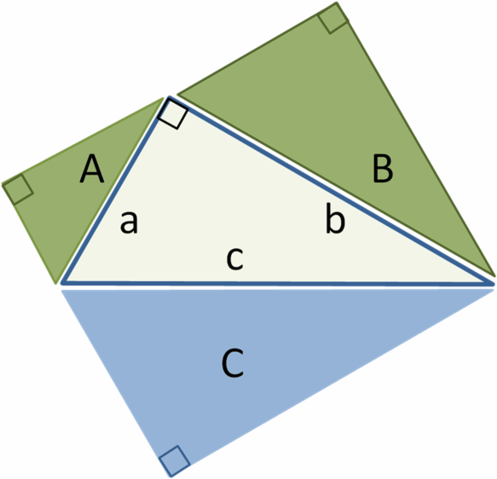
Description	English: A similarity proof for Pythagoras' theorem based upon areas proportional to sides on the center triangle. Area of triangle C = sum of areas of A and B. All three right triangles are similar, so all three areas are proportional to the side bordering the centre triangle. Hence, α(a² + b²) = α c², or dividing by α, we have Pythagoras' theorem.
Date	28 May 2010
Source	Own work
Author	Brews ohare

This math image could be recreated using vector graphics as an SVG file. This has several advantages; see Commons:Media for cleanup for more information. If an SVG form of this image is already available, please upload it. After uploading an SVG, replace this template with {{ vector version available|new image name.svg}}.

Licensing

I, the copyright holder of this work, hereby publish it under the following licenses:

This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

You are free:

to share – to copy, distribute and transmit the work
to remix – to adapt the work

Under the following conditions:

attribution – You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work).
share alike – If you alter, transform, or build upon this work, you may distribute the resulting work only under the same or similar license to this one.

CC-BY-SA-3.0 truetrue

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.

http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue

You may select the license of your choice.

File usage

The following pages on Schools Wikipedia link to this image (list may be incomplete):

Pythagorean theorem

Wikipedia for Schools...

Through Schools Wikipedia, SOS Children's Villages has brought learning to children around the world. SOS Children is an international children's charity, providing a good home and loving family to thousands of children who have lost their parents. We also work with communities to help vulnerable families stay together and raise children in the best possible environment. Find out how you can help children in other countries.