University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions"

Study the idempotent identities of Theorem 1 on pages SF-2 and SF-3. An idempotent is an object A such that (A operation A) = A. The idempotent laws for union and intersection are: A 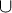\cup A = A, A \cap A = A. Prove several of the idempotent identities.
Click https://s3.amazonaws.com/saylordotorg-resources/wwwresources/site/wp-content/uploads/2011/09/CS202-Sets-and-Functions-Edward-Benderand-S.-Gill-Williamson.pdf link to open resource.