University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions"

Study the notation used for sets in Section 1 on pages SF-1 to SF-2.

A set is a collection of elements, called members of the set. Sets are denoted using capital letters; elements are denoted using small letters. We write a ∈ A for a an element of A; and a 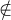\notin A, for a not an element of A. Examples of sets can be found everywhere. All the units in this course comprise a set. The collection of people related to you comprise a set. Sets can be described using English descriptions, predicates in logic, or mathematical functions, in particular Boolean functions. A set can also be defined by listing the members of the set. A set can be finite, having a finite number of members; a set can be infinite. The number of elements of a set is one obvious property of a set.

The members, or elements, of a set can be anything, even sets themselves. For example, {a, b, {a, b}} is a set of 3 members, and one of the members is a set.
Click https://s3.amazonaws.com/saylordotorg-resources/wwwresources/site/wp-content/uploads/2011/09/CS202-Sets-and-Functions-Edward-Benderand-S.-Gill-Williamson.pdf link to open resource.