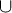CS202: Discrete Structures

5.3: Set Identities and Proof of Set Identities

• University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

  Read "Set Properties and Proofs" on pages SF-2 - SF-6.
  

• 5.3.1: Commutative Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study Theorem 1, on pages SF-2 and SF-3, on the commutative laws: A $\cap$ B = B $\cap$ A, A $\cup$ B = B $\cup$ A. Prove the commutative laws.

• 5.3.2: Associative Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study Theorem 1 on pages SF-2 and SF-3 on the associative laws: (A $\cap$ B) $\cap$ C = A $\cap$ (B $\cap$ C) = A $\cap$ B $\cap$ C. Note that we can write the rightmost expression, which has no parenthesis, because $\cap$ is associative. Replacing $\cap$ by the intersection operations, gives the associative law for intersection. Prove the associative laws.

• 5.3.3: Distributive Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study Theorem 1 on pages SF-2 and SF-3 on the distributive laws: A $\cap$ (B $\cup$ C) = (A $\cap$ B) $\cup$ (A $\cap$ C); A $\cup$ (B $\cap$ C) = (A $\cup$ B) $\cap$ (A $\cup$ C). The former shows union distributes over intersection; and the latter shows intersection distributes over union. Prove the distributive laws. 

• 5.3.4: Identity Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study the identities (equality of two set expressions) on pages SF-3 and SF-4 (the top of SF-3 and examples 2, 3, and 4). It follows from the definition of the empty set that A $\cup$ Ø = A, A $\cap$ Ø = Ø. Prove these identities.

• 5.3.5: Complement Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study the identities involving complement on pages SF-3 and SF-4. For universal set E, E' = Ø= A ∩ A'; A - A = Ø. Study example 1 on SF-4; VENN diagrams are a visual representation of sets, which are useful for depicting set membership of complements as well as other sets resulting from set operations. Use a VENN diagram to prove one of the identities involving complement.

• 5.3.6: Double Complement Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study Theorem 1 on pages SF-2 and SF-3. Double complement is also referred to as double negative: (A') ' = A. Take the identities in the theorem involving set difference or complement. Insert a second difference or complement operator, thus creating some new set equations, and check whether the new set equations are still identities. Prove or disprove several of the equations you created by adding a second difference or complement operation.

• 5.3.7: Idempotent Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study the idempotent identities of Theorem 1 on pages SF-2 and SF-3. An idempotent is an object A such that (A operation A) = A. The idempotent laws for union and intersection are: A $\cup$ A = A, A $\cap$ A = A. Prove several of the idempotent identities.

• 5.3.8: Universal Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study the identities involving the universal set in Theorem 1 and in examples 1 and 2 on pages SF-2 to SF-4. Prove some of the identities involving the universal set.

• 5.3.9: DeMorgan's Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

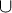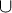    Study Theorem 1 on pages SF-2 and SF-3 on DeMorgan's laws: (A $\cup$ B) ' = A' $\cap$ B'; (A $\cap$ B)' = A' $\cup$ B'. In English, the complement of A union B is the intersection of A complement and B complement; and the complement of A intersect B is the complement of A union the complement of B. DeMorgan's laws are famous and appear in many places in mathematics, engineering, and computer science. Prove DeMorgan's Laws.

• 5.3.10: Absorption Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study Theorem 1 on pages SF-2 and SF-3 on absorption laws. These are called absorption identities because one of the sets is absorbed by the other(s). Prove the absorption laws.

• 5.3.11: Set Difference Laws

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study pages SF-1 and SF-2, and Theorem 1 on pages SF-2 and SF-3. The set difference laws: A - (B U C) = (A - B) ∩ (A - C);  A - (B ∩ C) = (A - B) U (A - C) follow from the definition of set difference and De Morgan's Laws (use the fact the A - B = A ∩ B').