• 5.1: Definition of Set Theory

      • 5.1.1: Set Notation

        • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

          Study the notation used for sets in Section 1 on pages SF-1 to SF-2.

          A set is a collection of elements, called members of the set. Sets are denoted using capital letters; elements are denoted using small letters. We write a ∈ A for a an element of A; and a 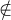\notin A, for a not an element of A. Examples of sets can be found everywhere. All the units in this course comprise a set. The collection of people related to you comprise a set. Sets can be described using English descriptions, predicates in logic, or mathematical functions, in particular Boolean functions. A set can also be defined by listing the members of the set. A set can be finite, having a finite number of members; a set can be infinite. The number of elements of a set is one obvious property of a set.

          The members, or elements, of a set can be anything, even sets themselves. For example, {a, b, {a, b}} is a set of 3 members, and one of the members is a set.

      • 5.1.2: Set Equality

        • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

          Study Definition 1 on page SF-1. Typically, when an object is defined in mathematics, we next define when two of those objects are equal. Then we define operations on those objects. Now, for the objects are sets. When are two sets equal?

          If A and B are sets, and if a ∈ A, implies a ∈ B, then we say A is a subset of B, denoted A \subset  B. The number of subsets of a set A, is denoted 2A (the reason for this notation will become clear when you study functions.)

          A = B, if and only if, A \subset  B and B \subset  A. A and B are assumed to be subsets of a universal set E. Ø is the empty set or the set that has no members.

          Note that the order of the elements in a set does not change the set. Work sufficient examples to ensure that you completely understand the concept of set equality.