Section 3
Quantum Mechanical Description of the Atomic Orbital
Book
Version 33
By Boundless
By Boundless
Boundless Chemistry
Chemistry
by Boundless
6 concepts
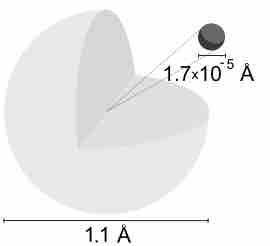
Description of the Hydrogen Atom
A hydrogen atom is electrically neutral, containing a single proton and a single electron bound to the nucleus by the Coulomb force.
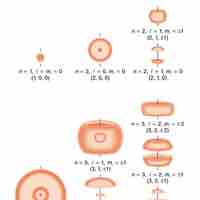
Indeterminacy and Probability Distribution Maps
Quantum indeterminacy refers to the necessary incompleteness in the description of a physical system.
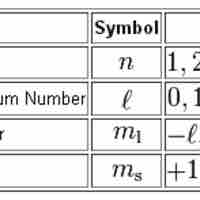
Quantum Numbers
Quantum numbers provide a numerical description of the orbitals in which electrons reside.
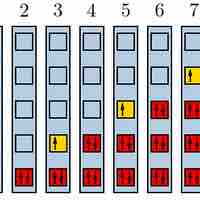
The Pauli Exclusion Principle
The Pauli exclusion principle states that no two fermions can have identical wavefunctions.
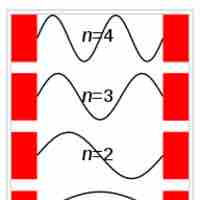
Particle in a Box
The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically.
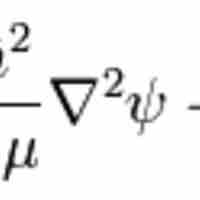
Wave Equation for the Hydrogen Atom
The hydrogen atom is the simplest one-electron atom and has analytical solutions to the Schrödinger equation.