Convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence, or divergence of an infinite series. When testing the convergence of a series, you should remember that there is no single convergence test which works for all series. It is up to you to guess and pick the right test for a given series. Practice and training will help you in expediting this "guessing" process.
Here is a summary for the convergence test that we have learned:
List of Tests
Limit of the Summand: If the limit of the summand is undefined or nonzero, then the series must diverge.
Ratio test: For
Root test: For
Integral test: For a positive, monotone decreasing function
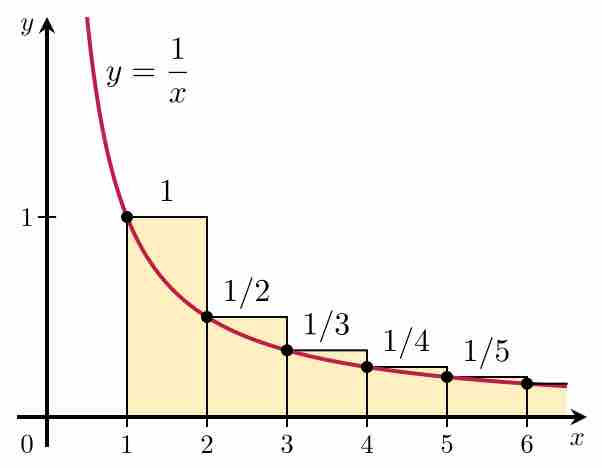
Integral Test
The integral test applied to the harmonic series. Since the area under the curve
Direct comparison test: If the series
Limit comparison test: If