Section 4
Applications of Integration
By Boundless
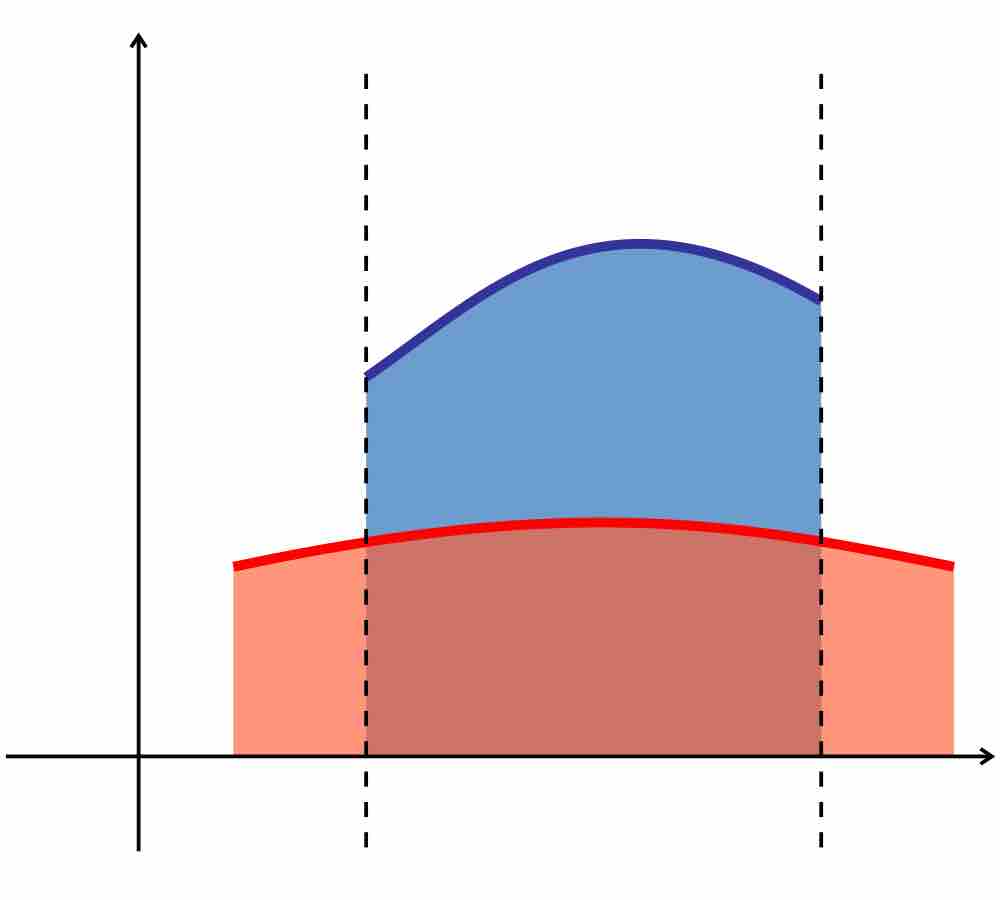
The area between the graphs of two functions is equal to the integral of a function,

Volumes of complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary.
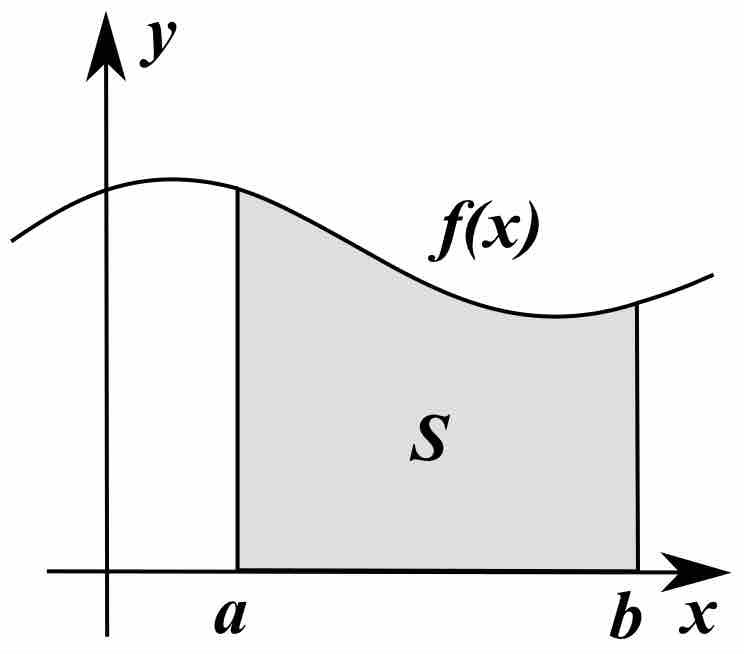
The average of a function
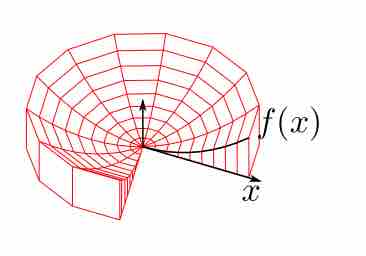
In the shell method, a function is rotated around an axis and modeled by an infinite number of cylindrical shells, all infinitely thin.
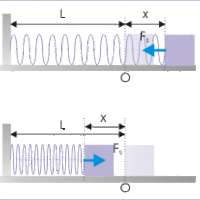
Forces may do work on a system. Work done by a force (
Disc and shell methods of integration can be used to find the volume of a solid produced by revolution.