A study of limits and continuity in multivariable calculus yields many counter-intuitive results not demonstrated by single-variable functions . For example, there are scalar functions of two variables with points in their domain which give a particular limit when approached along any arbitrary line, yet give a different limit when approached along a parabola. For example, the function
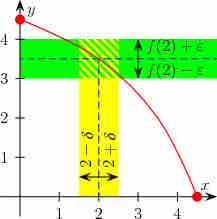
Continuity
Continuity in single-variable function as shown is rather obvious. However, continuity in multivariable functions yields many counter-intuitive results.
Continuity in each argument does not imply multivariate continuity. For instance, in the case of a real-valued function with two real-valued parameters,
It is easy to check that all real-valued functions (with one real-valued argument) that are given by