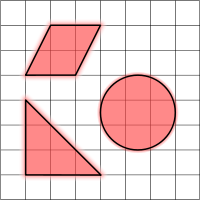
Area
Did you know...
The articles in this Schools selection have been arranged by curriculum topic thanks to SOS Children volunteers. Child sponsorship helps children one by one http://www.sponsor-a-child.org.uk/.
Area is a quantity expressing the two- dimensional size of a defined part of a surface, typically a region bounded by a closed curve. The term surface area refers to the total area of the exposed surface of a 3-dimensional solid, such as the sum of the areas of the exposed sides of a polyhedron.
Units
Units for measuring surface area include:
- Metric
- square metre (m²) = SI derived unit
- are (a) = 100 square metres (m²)
- hectare (ha) = 10,000 square metres (m²)
- square kilometre (km²) = 1,000,000 square metres (m²)
- square megametre (Mm²) = 1012 square metres (m²)
- US & Imperial Units
- square foot = 144 square inches = 0.09290304 square metres (m²)
- square yard = 9 square feet = 0.83612736 square metres (m²)
- square perch = 30.25 square yards = 25.2928526 square metres (m²)
- acre = 160 square perches or 4,840 square yards or 43,560 square feet = 4046.8564224 square metres (m²)
- square mile = 640 acres = 2.5899881103 square kilometres (km²)
Useful formulas
| Shape | Equation | Variables |
|---|---|---|
| Square | 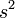 |
 is the length of the side of the square. is the length of the side of the square. |
| Regular triangle | 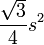 |
 is the length of one side of the triangle. is the length of one side of the triangle. |
| Regular hexagon | 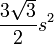 |
 is the length of one side of the hexagon. is the length of one side of the hexagon. |
| Regular octagon | 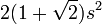 |
 is the length of one side of the octagon. is the length of one side of the octagon. |
| Any regular polygon | 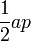 |
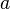 is the apothem, or the radius of an inscribed circle in the polygon, and is the apothem, or the radius of an inscribed circle in the polygon, and 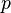 is the perimeter of the polygon. is the perimeter of the polygon. |
| Any regular polygon | 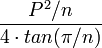 |
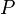 is the Perimeter and is the Perimeter and 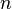 is the number of sides. is the number of sides. |
| Any regular polygon (using degree measure) | 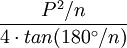 |
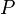 is the Perimeter and is the Perimeter and 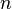 is the number of sides. is the number of sides. |
| Rectangle | 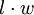 |
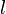 and and 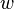 are the lengths of the rectangle's sides (length and width). are the lengths of the rectangle's sides (length and width). |
| Parallelogram (in general) | 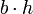 |
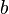 and and 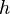 are the length of the base and the length of the perpendicular height, respectively. are the length of the base and the length of the perpendicular height, respectively. |
| Rhombus | 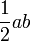 |
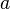 and and 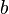 are the lengths of the two diagonals of the rhombus. are the lengths of the two diagonals of the rhombus. |
| Triangle | 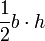 |
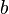 and and 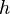 are the base and altitude (measured perpendicular to the base), respectively. are the base and altitude (measured perpendicular to the base), respectively. |
| Triangle | 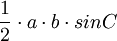 |
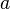 and and 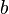 are any two sides, and are any two sides, and 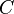 is the angle between them. is the angle between them. |
| Circle | 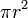 , or , or 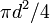 |
 is the radius and is the radius and 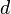 the diameter. the diameter. |
| Ellipse | 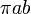 |
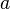 and and 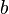 are the semi-major and semi-minor axes, respectively. are the semi-major and semi-minor axes, respectively. |
| Trapezoid | 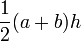 |
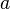 and and 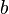 are the parallel sides and are the parallel sides and 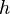 the distance (height) between the parallels. the distance (height) between the parallels. |
| Total surface area of a Cylinder | 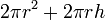 |
 and and 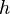 are the radius and height, respectively. are the radius and height, respectively. |
| Lateral surface area of a cylinder | 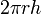 |
 and and 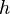 are the radius and height, respectively. are the radius and height, respectively. |
| Total surface area of a Cone | 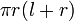 |
 and and 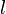 are the radius and slant height, respectively. are the radius and slant height, respectively. |
| Lateral surface area of a cone | 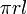 |
 and and 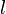 are the radius and slant height, respectively. are the radius and slant height, respectively. |
| Total surface area of a Sphere | 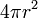 or or 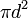 |
 and and 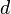 are the radius and diameter, respectively. are the radius and diameter, respectively. |
| Total surface area of an ellipsoid | See the article. | |
| Circular sector | 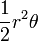 |
 and and 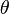 are the radius and angle (in radians), respectively. are the radius and angle (in radians), respectively. |
| Square to circular area conversion | 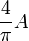 |
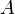 is the area of the square in square units. is the area of the square in square units. |
| Circular to square area conversion | 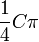 |
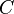 is the area of the circle in circular units. is the area of the circle in circular units. |
All of the above calculations show how to find the area of many shapes.