CS202: Discrete Structures

5.2: Set Operations

• Recall that in logic, operations for building compound statements were defined. We do the same for sets, i.e. define operations for building new sets from old sets.
  

• 5.2.1: The Union Operator

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study set operations and the property of set operations Section 1 on pages SF-2 - SF-3. Set Union is defined on page SF-2. 
    

    Set Union is defined on page SF-2. Note that A 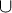$\cup$ B = {x : x ∈ A or x ∈ B}. You will read and reread this section several times, each time focusing on a basic set operation. These basic operations are so fundamental and ubiquitous (i.e. occur so frequently in mathematics, computer science, and their applications) that they deserve more than a quick reading. Work a lot of examples.
    

• 5.2.2: The Difference Operator

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    This reading is the same as that for the previous section. For this section, study the definitions of complement and set difference on page SF-2.

    A-B = {x : x ∈A and x $\notin$ B}, is called set difference, or the complement of B with respect to A.

• 5.2.3: The Intersection Operator

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Study the reading on set intersection, defined on page SF-2. Note: A ∩ B = {x : x ∈ A and x ∈ B}.

• 5.2.4: The Complement of a Set

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    This time, focus on complement of a set. Complement is set difference with respect to the largest set, called the universal set, namely, E - A is the complement of A. E is the universal set, the set of all elements; when sets are defined, the type of the elements is specified. For example, in a set of all red cars, the type of the members in this example, is car. We also say that the domain of the elements is the (universal) set of all cars.

• 5.2.5: Cartesian Products

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    One last time, look over the above reading. Now study the product of sets defined on page SF-2, just before the section titled "Set Properties and Proofs." The Cartesian Product, A x B = {(a, b) : a ∈ A and b ∈ B}, is referred to as the set of ordered pairs of A and B. Clearly, it is analogous to multiplication of numbers.

• 5.2.6: Binary Relation

  • University of California, San Diego: Edward Bender and S. Williamson's "Sets, Equivalence and Order: Sets and Functions" URL

    Given a set A, a binary relation, R on A, is a subset of A x A. Note that a binary relation is a set of order pairs (x, y) where x and y are in A. The next subunits define properties of a binary relation, reflexive and symmetric. A third property is transitivity.

    Relations are another critically important concept in set theory, functions, science, and every other subject. Work a lot of examples.

    A binary relation on A is reflexive, if (a, a) ∈ R.
    

    A binary relation is symmetric if (a, b) ∈ R, then (b, a) ∈ R.
    

    A binary relation is transitive if (a, b) ∈ R, (b, c) ∈ R, then (a, c ) ∈ R. There is an important consequence of a binary relation being reflexive, symmetric, and transitive. A binary relation that has all 3 properties is called an equivalence relation. If a binary relation on A is an equivalence relation, it determines a partition of A. A partition of A is a set of subsets of A, which are mutually disjoint, and whose union is A.