Section 2
The Chi-Squared Test
By Boundless
The multinomial experiment is the test of the null hypothesis that the parameters of a multinomial distribution equal specified values.
The chi-square test is used to determine if a distribution of observed frequencies differs from the theoretical expected frequencies.

Fisher's exact test is preferable to a chi-square test when sample sizes are small, or the data are very unequally distributed.
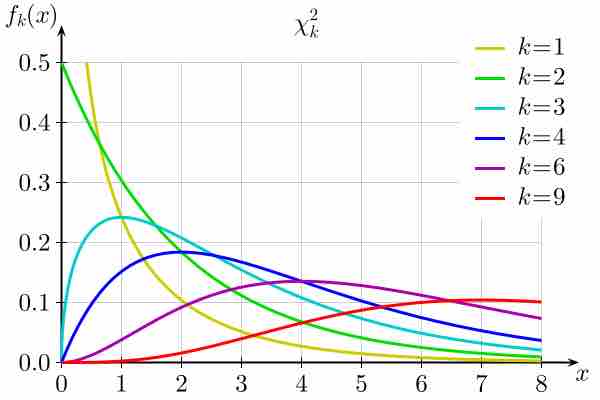
The goodness of fit test determines whether the data "fit" a particular distribution or not.
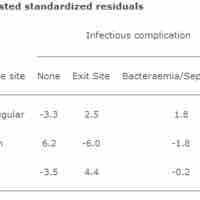
The chi-square test of association allows us to evaluate associations (or correlations) between categorical data.
The Chi-square test for goodness of fit compares the expected and observed values to determine how well an experimenter's predictions fit the data.
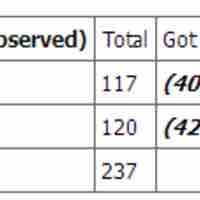
The chi-square test for independence is used to determine the relationship between two variables of a sample.