A system of equations consists of two or more equations with two or more variables, where any solution must satisfy all of the equations in the system at the same time.
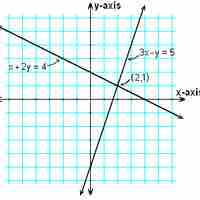
A simple way to solve a system of equations is to look for the intersecting point or points of the equations. This is the graphical method.
The substitution method is a way of solving a system of equations by expressing the equations in terms of only one variable.
The elimination method is used to eliminate a variable in order to more simply solve for the remaining variable(s) in a system of equations.
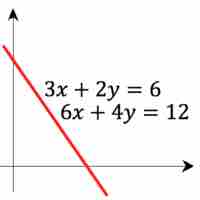
For linear equations in two variables, inconsistent systems have no solution, while dependent systems have infinitely many solutions.
Systems of equations can be used to solve many real-life problems in which multiple constraints are used on the same variables.