Leading Term, Leading Coefficient and Leading Test
All polynomial functions of first or higher order either increase or decrease indefinitely as
- If
$n$ is odd and$a_n$ is positive, the function declines to the left and inclines to the right. - If
$n$ is odd and$a_n$ is negative, the function inclines to the left and declines to the right. - If
$n$ is even and$a_n$ is positive, the function inclines both to the left and to the right. - If
$n$ is even and$a_n$ is negative, the function declines both to the left and to the right.
Examples
Consider the polynomial
In the leading term,
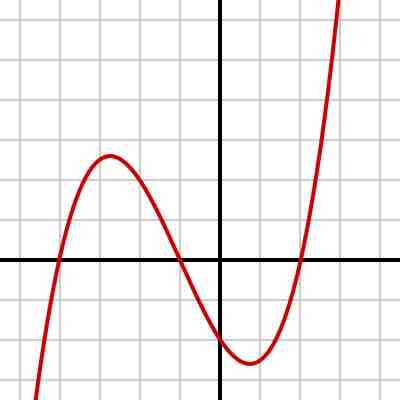
A polynomial of degree $3$
Graph of a polynomial with equation
Another example is the function
which has
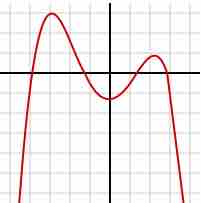
A polynomial of degree 4
Graph of
The Leading Test Explained
Intuitively, one can see why we need to look at the leading coefficient to see how a polynomial behaves at infinity: When
In general, when we have a polynomial
and the absolute value of
Now
Thus,