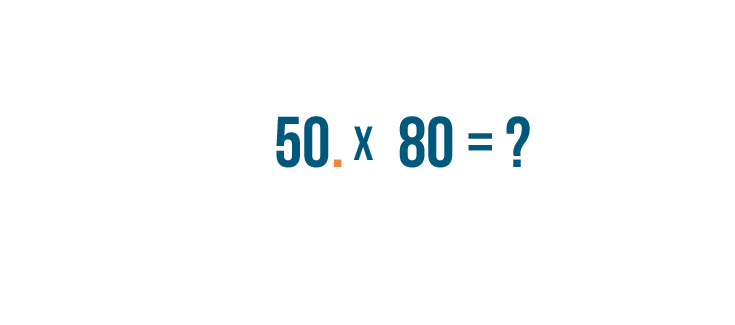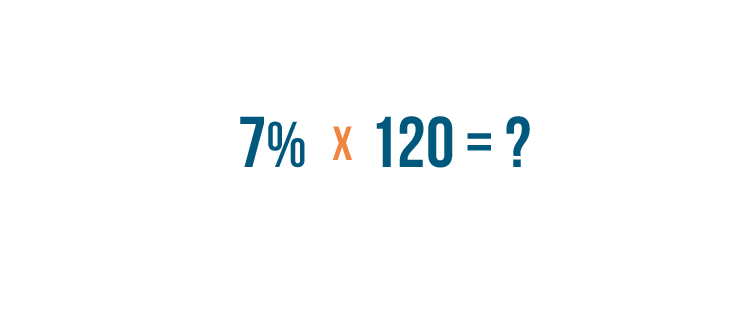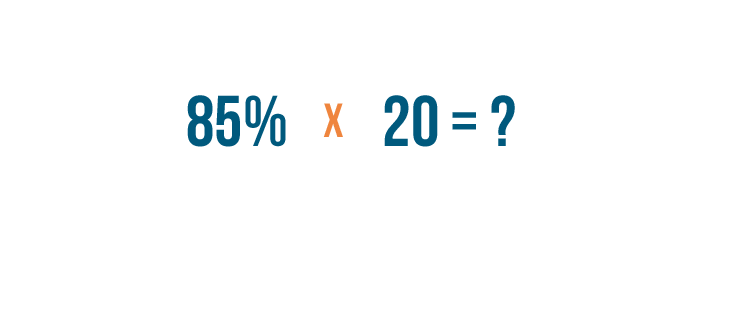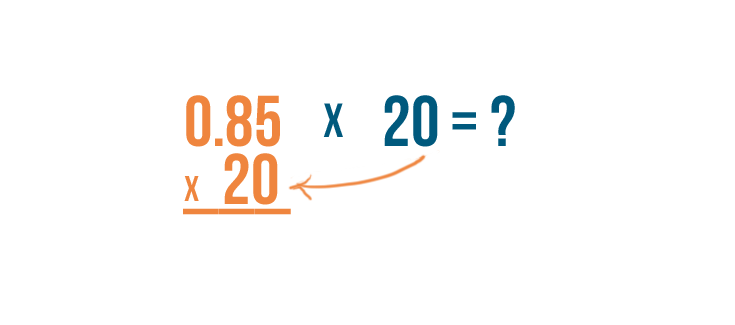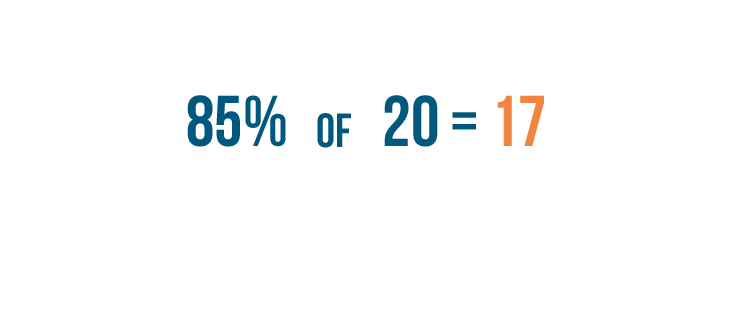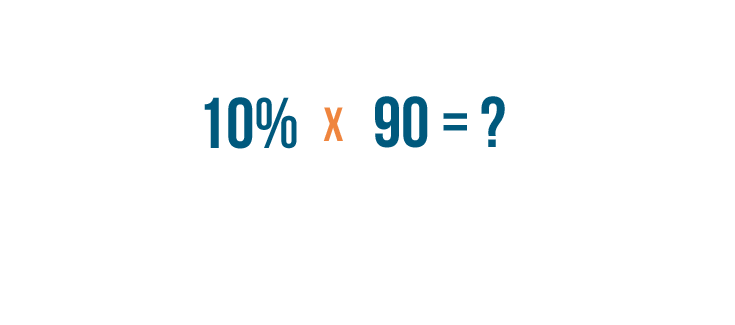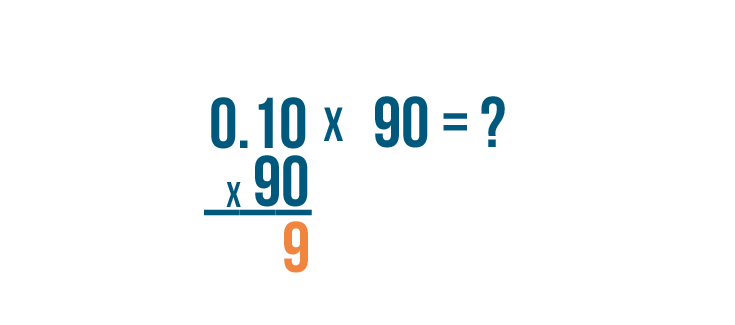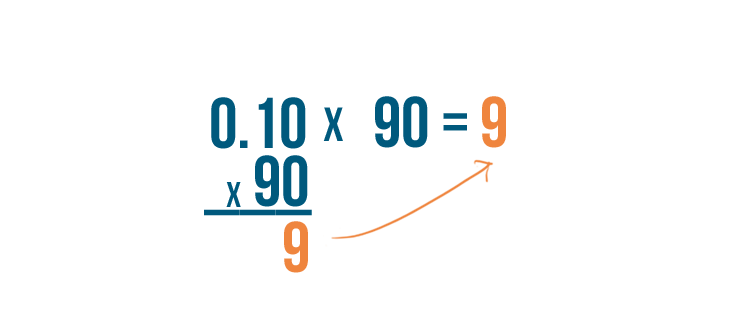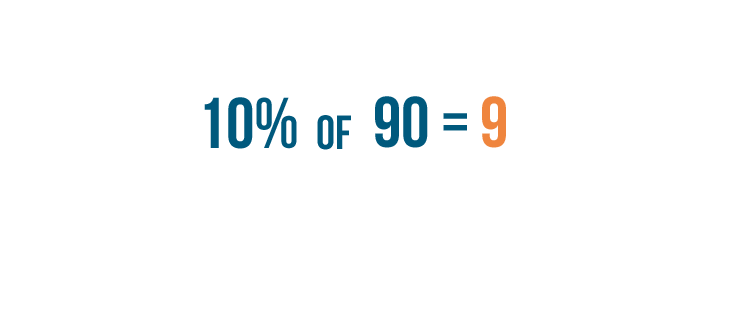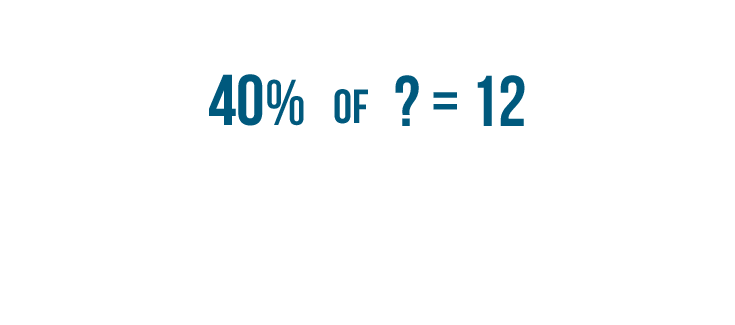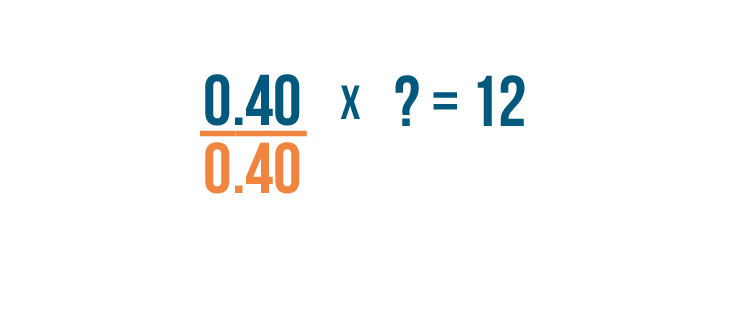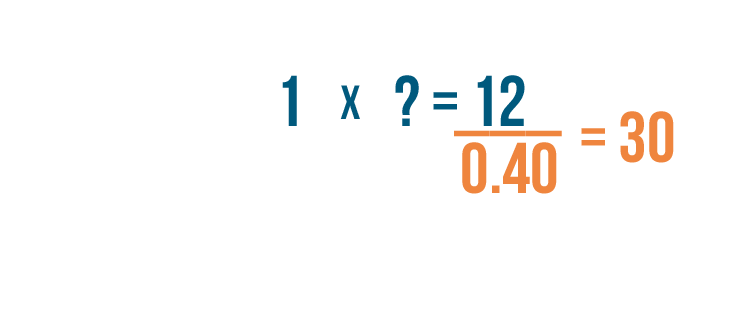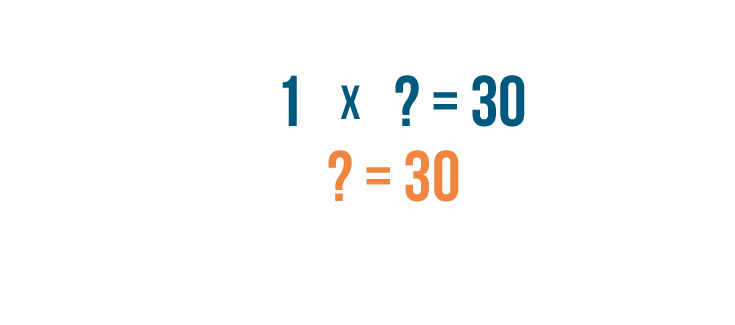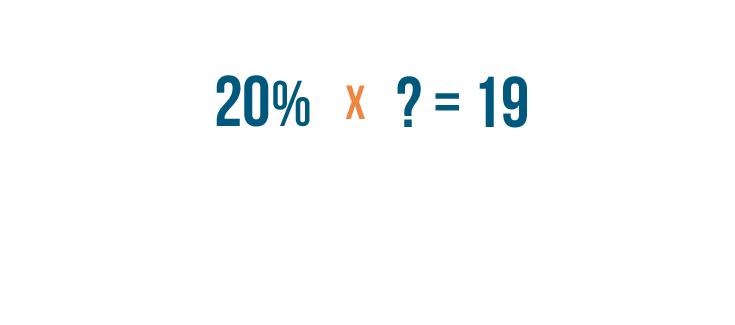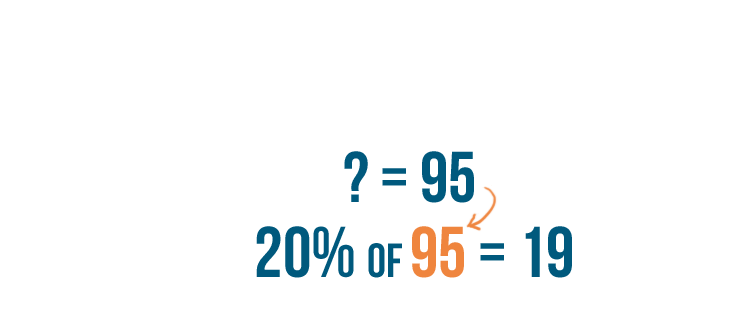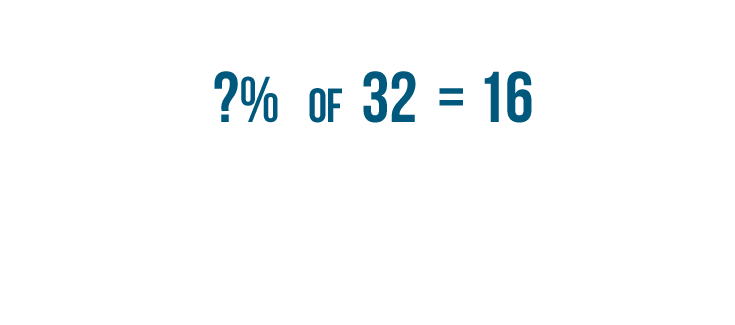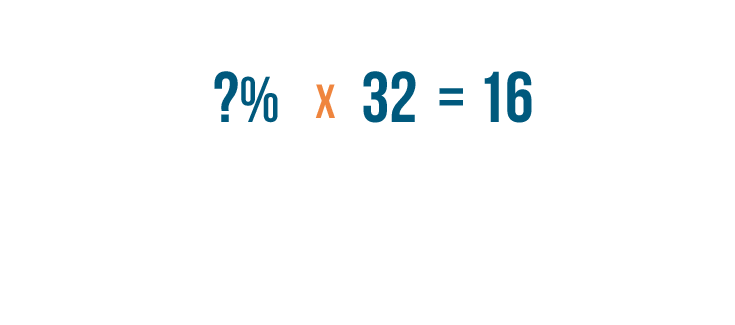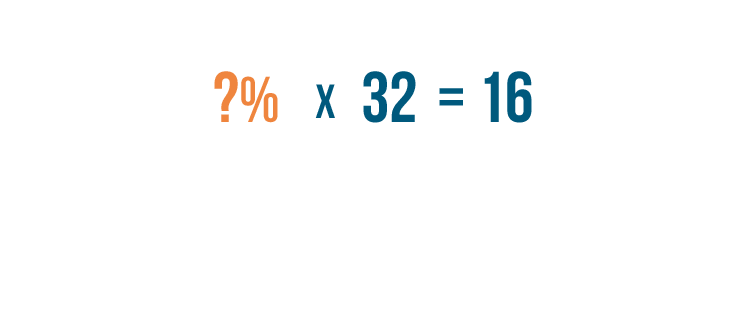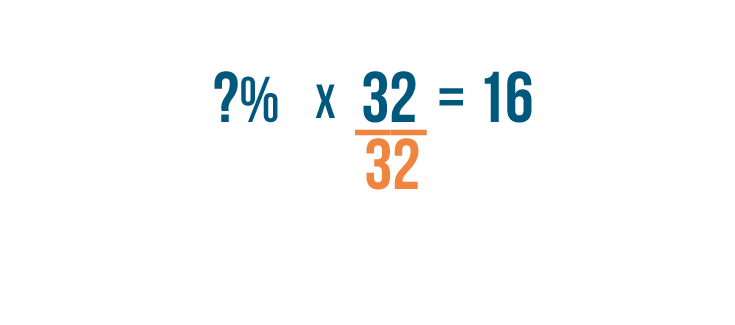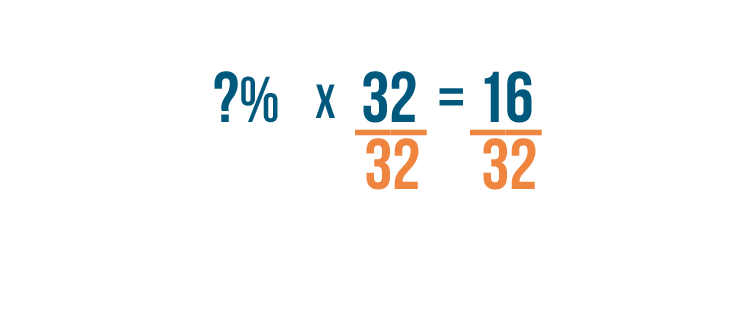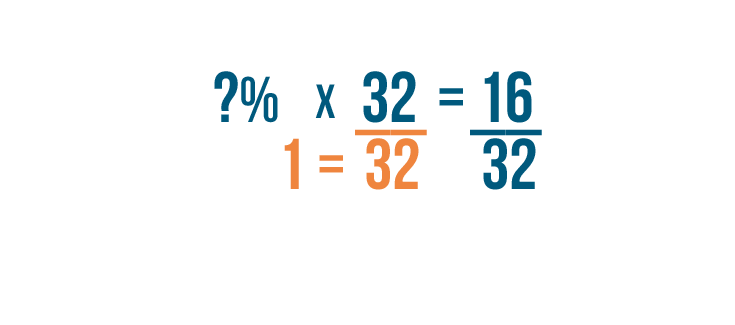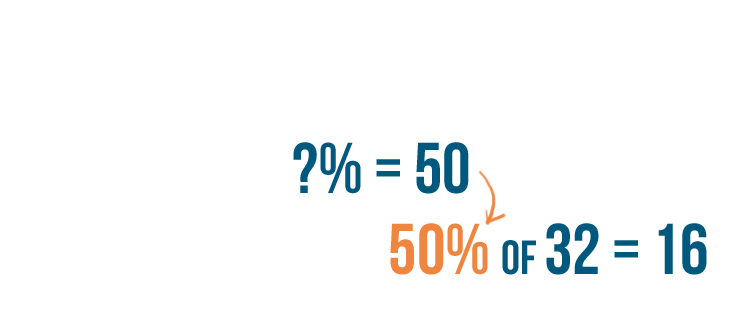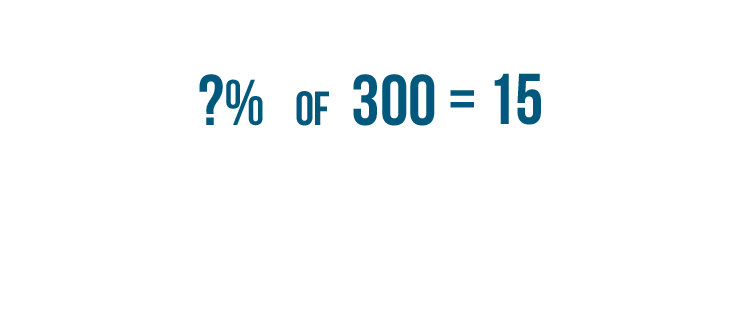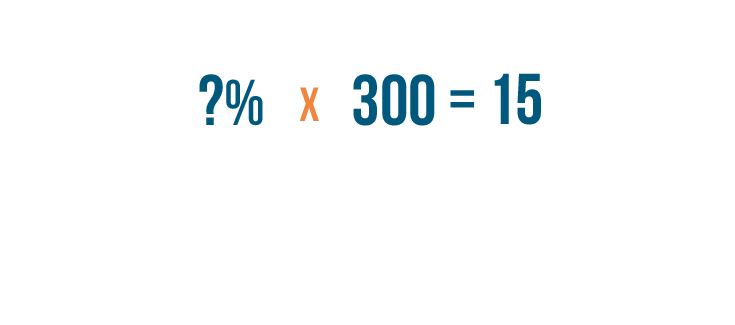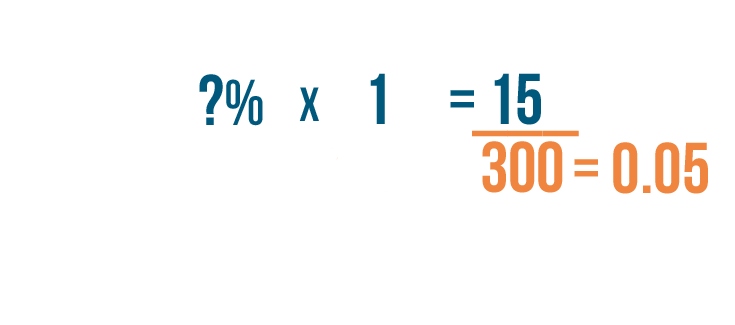Calculating percent problems

There are many times in real life when you may need to calculate a percentage. You might need to figure out how much money a 5% discount will save you, or how much interest you'll pay on a loan with a 6% interest rate . Knowing how to calculate percentages will help you in both of these situations.

Setting up the calculation

Let's say the mailing department was responsible for 25% of the accidents at your company this year. There were 80 accidents total, and 20 of them were in the mailing department. You could write that like this:

25% of 80 = 20

This expression tells you that 25% of 80 is equal to 20 . But what if you don't know how much a percentage is equal to? Let's say the demolition department was responsible for 50% of the 80 accidents. You don't know how many accidents 50% of 80 is. So you could write that like this:

50% of 80 = ?

To figure out what 50% of 80 is, you'll need to rewrite this example so it can be solved with math.

Click through the slideshow to see how to set up the example as a mathematical expression.

• 

  We need to turn this example into something we can solve with math.

• 

  First, we'll deal with the word of . Whenever you see that word in a percentage problem, it usually means multiplication .

• 

  First, we'll replace the word of with a multiplication sign.

• 

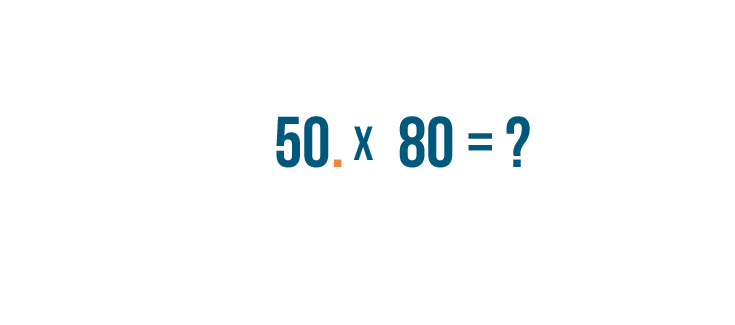
  Now we need to convert our percentage into a decimal. We'll do that by inserting a decimal point after the 50 ...

• 

  We'll do that by inserting a decimal point after the 50 ...and moving it two places to the left.

• 

  Now we have an equation we can use math to solve. All we have to do is multiply 0.50 by 80 .

• 

  Let's set up another example. This time we want to find 7% of 120 .

• 

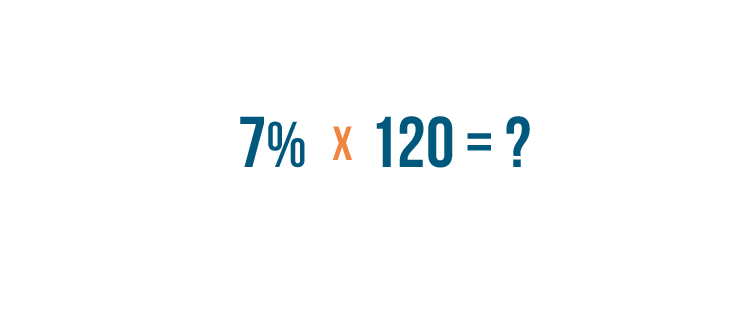
  First, we'll replace the word of with a multiplication sign.

• 

  We'll turn our percent into a decimal . We'll insert our decimal point after the 7 ...

• 

  We'll turn our percent into a decimal . We'll insert our decimal point after the 7 ...and move it two spaces to the left.

• 

  Now we've set up an equation we can solve with math.

• 

Finding how much a percent is worth

Let's imagine you scored 85% on your driving test. There were 20 questions on the test, and you want to figure out how many of them you got right. You just learned how to set up this example—now you'll learn how to solve it.

Click through the slideshow to learn how to find how much a percent is worth .

• 

  Before we start solving, let's set up our example as a mathematical expression .

• 

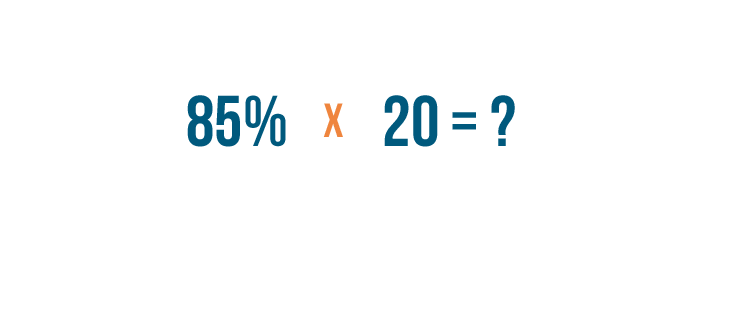
  We'll replace the word of with a multiplication sign.

• 

  Now we'll convert our percent to a decimal—and we're ready to start solving.

• 

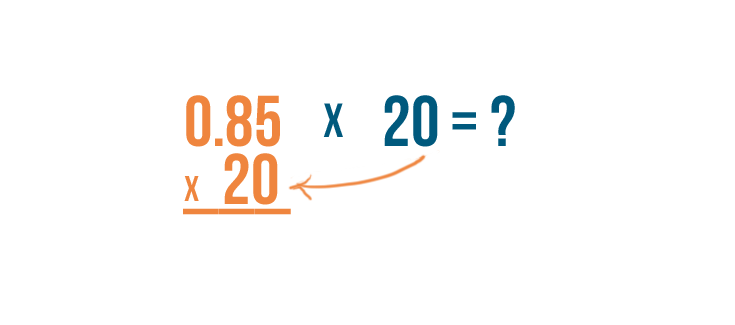
  All we have to do is multiply 0.85 by 20 .

• 

  0.85 times 20 is equal to 17 .

• 

  So 85% of 20 is 17 .

• 

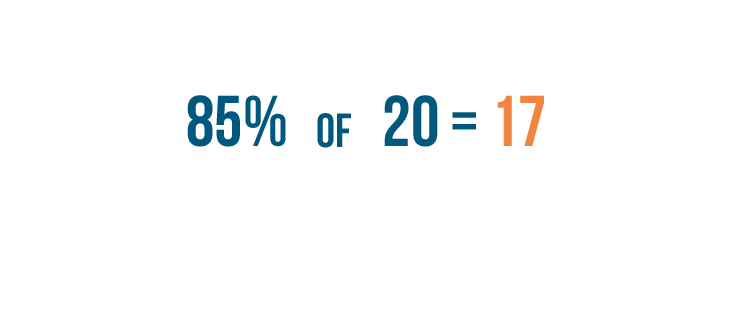
  This means you got 17 correct answers on your test.

• 

  Let's try another example. We want to find 10% of 90 .

• 

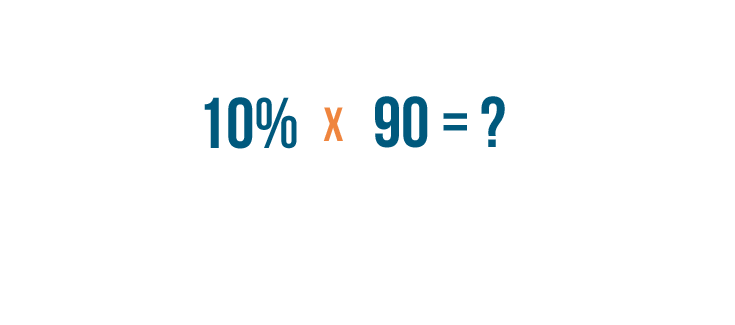
  First, we'll replace the word of with a multiplication sign.

• 

  Now we'll turn our percent into a decimal .

• 

  Now all we have to do is multiply 0.10 times 90 .

• 

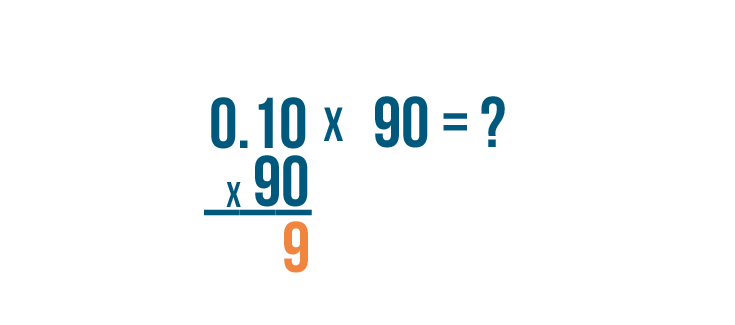
  0.10 times 90 is equal to 9 .

• 

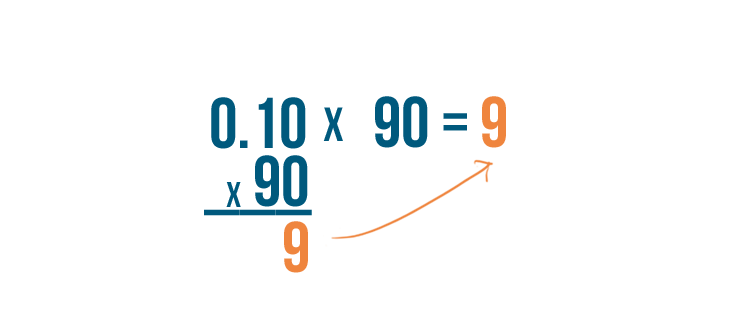
  Now we can replace the question mark in our problem with a 9 .

• 

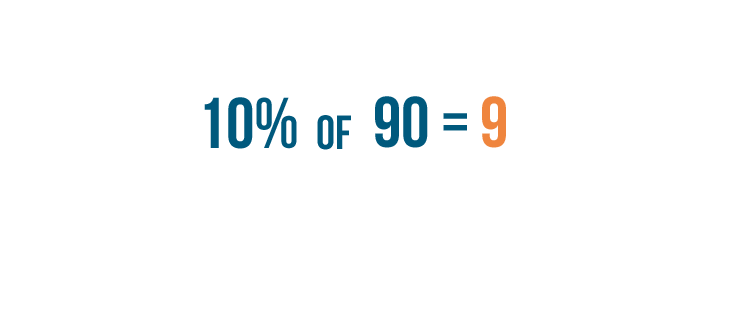
  So 10% of 90 equals 9 .

• 

Try This!

Use decimals to calculate how much these percentages are worth.

You have a coupon for 20% off the price of a book. If the book you want usually costs $10, how much is the coupon worth?

There are 200 families in your town. The newspaper reports that 47% of them have more than two children. How many families in town have more than two children?

Your doctor saw 170 new patients last year. 60% of new patients were women. How many new female patients did your doctor see last year?

Finding the total

Over the past week, 40% of the phone calls to Alicia's cell phone were from her son. Let's say you know that her son called her 12 times. Now you want to find out how many total calls she received. We can rewrite this example like this:

40% of ? = 12

This time we're missing the total —we don't know how many calls Alicia received.

Click through the slideshow to see how to find the total.

• 

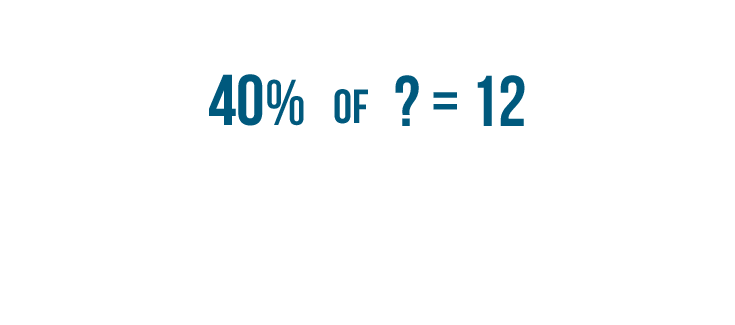
  We know that 12 is 40% of our missing total. We want to find out what the total is.

• 

  First, we'll replace the word of with a multiplication sign.

• 

  Then we'll turn the percent into a decimal by moving the decimal point two spaces to the left. Now our problem is ready to solve.

• 

  First, we'll have to get the missing number alone on one side of the equals sign so we'll know what it's equal to .

• 

  To get the missing number alone, we'll need to get rid of the 0.40 .

• 

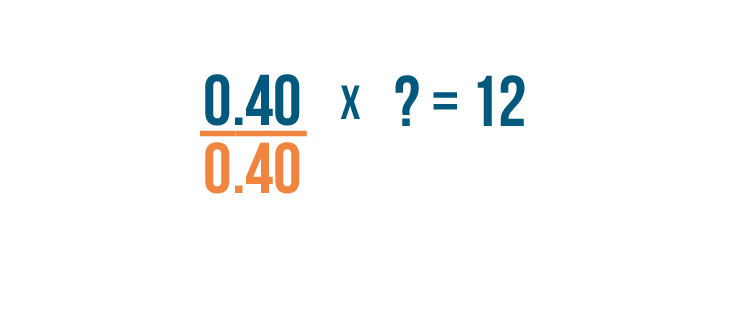
  We'll divide 0.40 by itself to get rid of it.

• 

  The equals sign means the two sides of the expression are equal , so we have to divide the other side by 0.40 too.

• 

  Let's start with the left side of the equation. 0.40 divided by 0.40 is equal to 1 .

• 

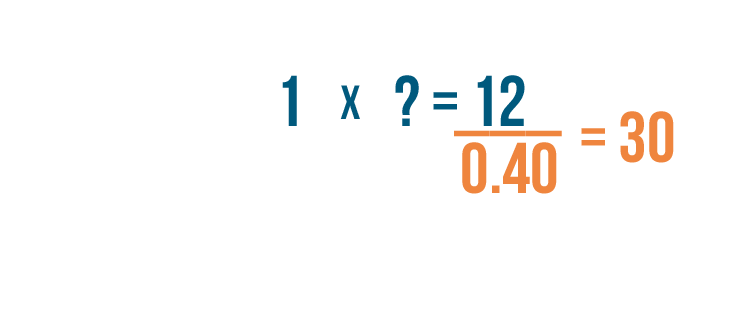
  We'll replace 0.40 with 1 . 12 divided by 0.40 equals 30 .

• 

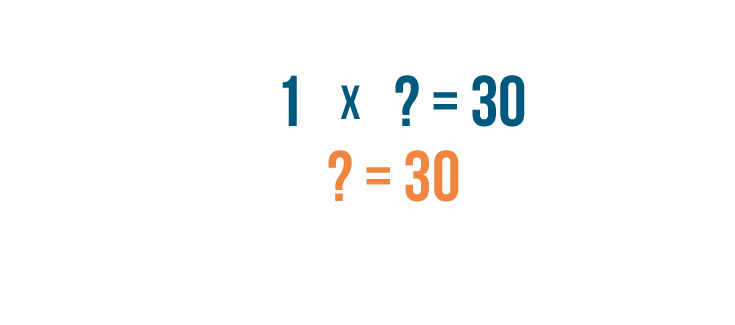
  Now we know that 1 times our missing number is equal to 30 . So our missing number is also equal to 30 .

• 

  We can replace the question mark in our original example with 30 . Now we know that 12 is 40% of 30 .

• 

  Let's try another example. 20% of a missing number is equal to 19 . We want to find the missing number.
  

• 

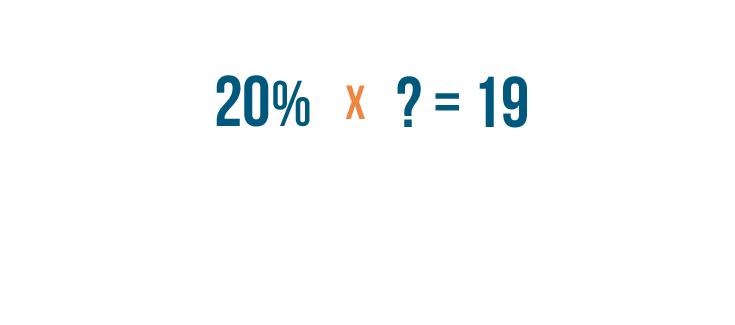
  Just like before, we'll replace the word of with a multiplication sign.

• 

  Next, we'll turn our percent into a decimal by moving the decimal point two spaces to the left.

• 

  Now we'll need to get our missing number alone on one side of the equals sign.

• 

  We'll divide 0.20 by itself to get rid of it. To keep the two sides equal, we'll have to divide the 19 by 0.20 too.

• 

  0.20 divided by 0.20 equals 1 .

• 

  We'll replace 0.20 with 1 and divide the other side of the equation. 19 divided by 0.20 equals 95 .

• 

  Now we can see that 1 times our missing number equals 95 . So our missing number is also equal to 95 .

• 

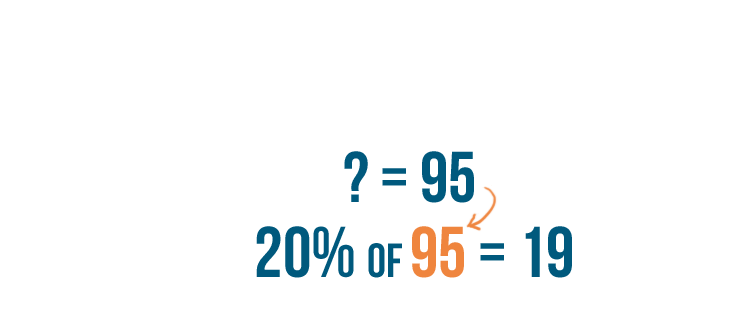
  We can replace the question mark in our original example with 95 . Now we know that 19 is 20% of 95 .

• 

Try This!

Find the missing whole in each of these problems.

Four students are sharing an apartment. Each pays 25% of the rent. If each student pays $200 per month, how much is the total rent for each month?

Jill has a 25% off coupon for some computer software. If the coupon saved her $35, how much would the software cost without the coupon?

Allen paid $12 in interest on his credit card this month. If you know that the interest rate on his card is 6%, how much was the total amount on his card?

Finding the percent

You just learned that 16 of your 32 cousins prefer chocolate ice cream to strawberry ice cream. You want to find out what percentage of your cousins likes chocolate ice cream. You can rewrite this example like this:

?% of 32 = 16

This time, the number we're missing is the percent . We want to know what percent is equal to 16 out of 32 .

Click through the slideshow to learn how to find the percent.

• 

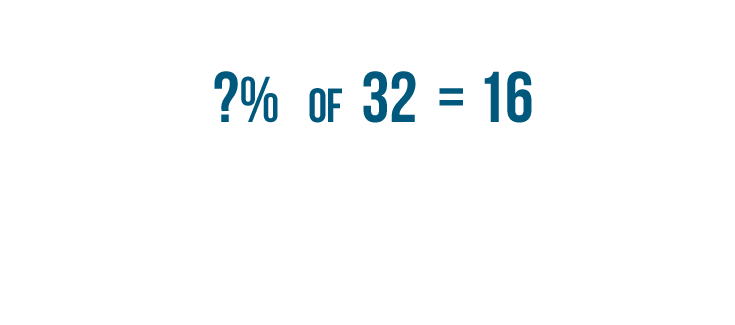
  We want to find out what percent of 32 is equal to 16 .

• 

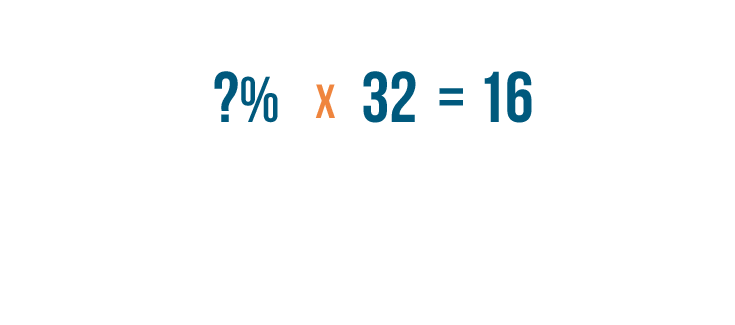
  First, we'll replace the word of with a multiplication sign.

• 

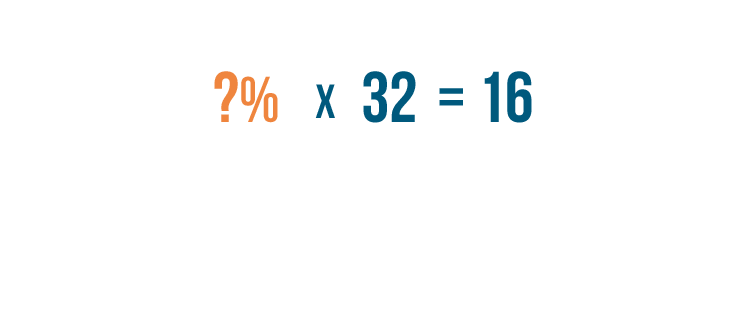
  This time, the percent is our missing number , so we can't turn it into a decimal. We'll leave it the way it is for now.

• 

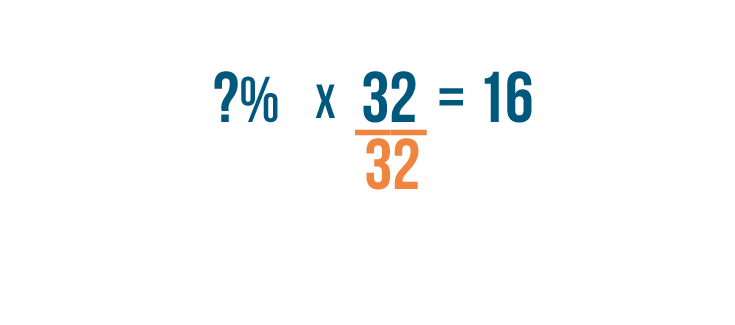
  To get the missing number alone on one side of the equation, we'll divide 32 by itself.

• 

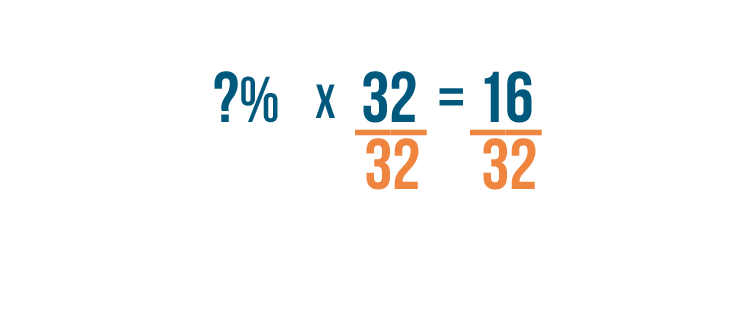
  To keep the two sides of the equals sign the same, we'll divide 16 by 32 too.

• 

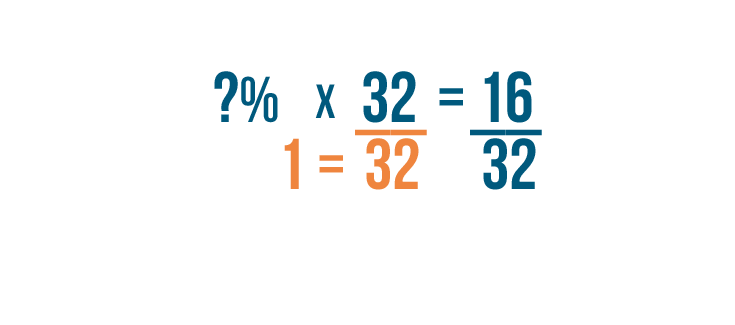
  32 divided by 32 equals 1 .

• 

  We'll replace 32 with 1 and divide the right side of the equation. 16 divided by 32 equals 0.50 .

• 

  Since our missing number times 1 is equal to 0.50 , our missing number is also equal to 0.50 .

• 

  We'll rewrite 0.50 as a percent by moving the decimal point two places to the right . 0.50 is equal to 50% .

• 

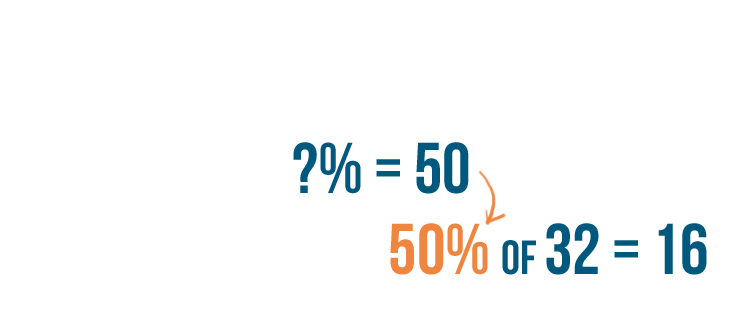
  Now we can replace the question mark in our example with 50 . So 16 is 50% of 32 .

• 

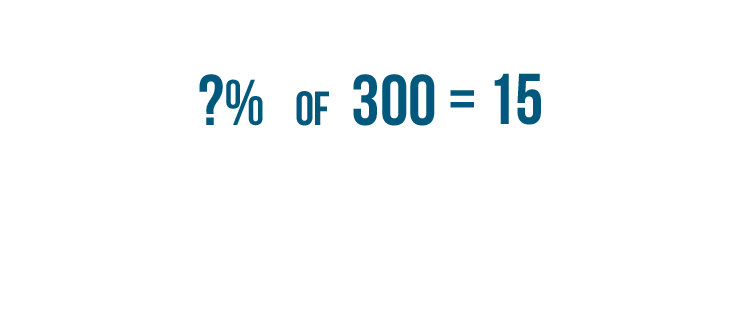
  Let's try another example. We're going to find what percent is equal to 15 out of 300 .

• 

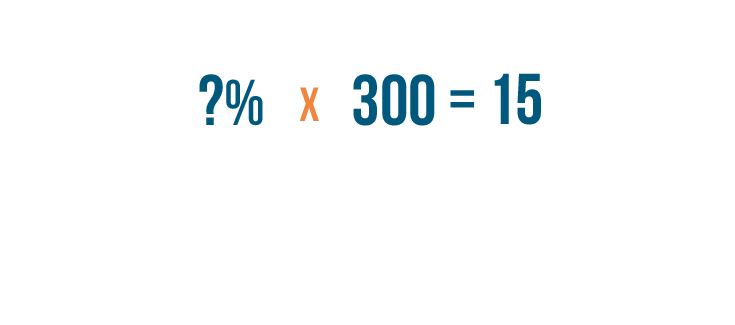
  First, we'll replace the word of with a multiplication sign.

• 

  Again, we're missing the percent. So we can't turn the percent into a decimal .

• 

  We'll divide 300 by itself to get rid of it. To keep the two sides of the equation equal, we'll have to divide 15 by 300 too.

• 

  Let's start with the left side of the equation. 300 divided by 300 equals 1 .

• 

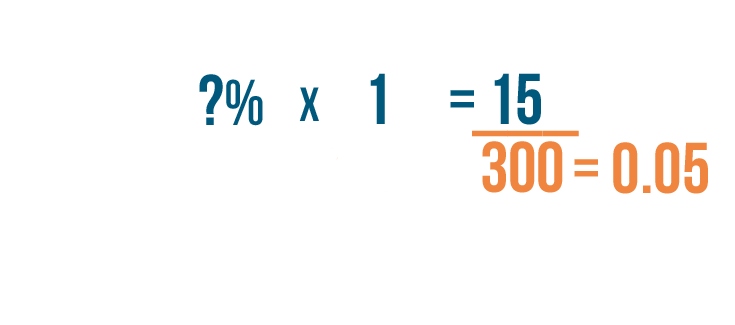
  We'll replace the 300 with a 1 . Now we'll divide the right side of the equation. 15 divided by 300 equals 0.05 .

• 

  Our missing number times 1 equals 0.05 . So our missing number is equal to 0.05 too.

• 

  Now we'll turn 0.05 into a percent by moving the decimal point two places to the right. 0.05 is equal to 5% .

• 

  Now we can replace the question mark in our original problem with 5%. So 15 is 5% of 300 .

• 

Try This!

Find the percent in each of these examples.

30 out of 50 of the stores in your neighborhood sell pickles. What percentage of the stores sell pickles?

There are 200 elderly people in your neighborhood. 80 of them don't know how to send text messages. What percentage of elderly people in your neighborhood don't know how to send texts?

Your local team has won 9 out of 45 basketball games in the past year. What percentage of games did the team win?